NÚMEROS RACIONAIS

Boa tarde pessoal, ontem não deu para publicar o assunto do 8° do Ensino Fundamental, então hoje vou publicar dois conteúdos, o do 8° e na sequência já estará disponível o conteúdo do 9° do Ensino Fundamental.

No assunto do 8° de hoje, vamos falar sobre os NÚMEROS RACIONAIS, sua definição, conceito, representação, transformações e o final estará disponível uma lista de exercícios de fixação.

NÚMEROS RACIONAIS

Definição

Os números racionais são os números que podem ser escritos na forma de fração. Esses números podem também ter representação decimal finita ou decimal infinita e periódica.

Representação

Os números Racionais são representados pela letra Q.

Observe que o conjunto dos números racionais, representado por Q , contém o conjunto dos números inteiros Z, que por sua vez contém o conjunto dos números naturais N. Então dizemos que N está contido em Z, que está contido em Q. Veja na imagem para ficar mais claro.

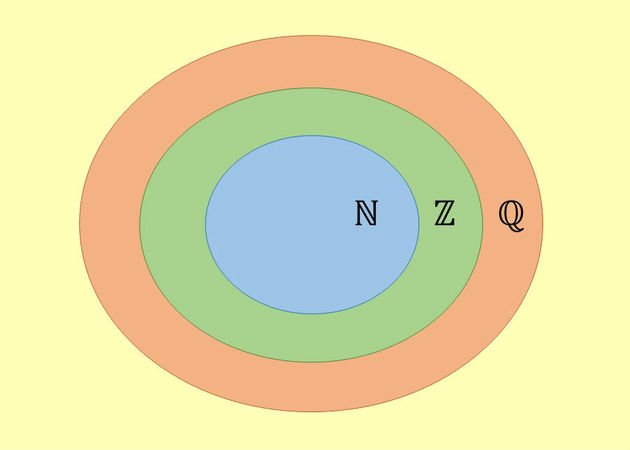
O conjunto dos números racionais pode ser representado por:

Obs.:  Z * quer dizer, todos do conjunto dos INTEIROS exceto o 0, pois não existe  frações onde o denominador é igual à 0.

Exemplos de Números Racionais

Números Inteiros

Números Decimais Exatos

Números Periódicos (Dízimas periódicas)

Subconjuntos do conjunto Q

Racionais não-nulos. Esse subconjunto é formado pelos números racionais sem o zero (0) .

Racionais não-negativos. Subconjunto composto pelos números racionais positivos e o zero..

Racionais não-positivos. Números racionais negativos e o zero formam esse subconjunto..

Racionais positivos. Esse subconjunto é composto pelos números racionais positivos.  .

Racionais negativos. Subconjunto formado pelos números racionais negativos..

Curiosidade

A letra que representa o conjunto dos números racionais, ou seja, o "Q" é derivado da palavra inglesa "quotient", que significa quociente.

Exercícios

1.     Assinale Verdadeiro (V) ou Falso (F):

a) 0,212121... é um número racional         (   )
b) 5/3 não é um número racional               (   )
c) -1 é um número racional                          (   )
d) O oposto de 13/5 é -13/5                        (   )
e) 1,41421356... é um número racional    (   )

2. Represente as frações em números decimais:

a) 375/200
b) 30/11
c) 3/5
d) 4/3
e) -7/50

Transformação de números decimais em frações decimais

Observe os seguintes números decimais:

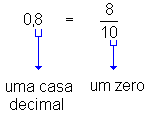
0,8 (lê-se "oito décimos"), ou seja,  .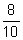

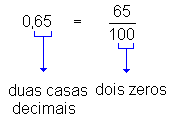
0,65 (lê-se "sessenta e cinco centésimos"), ou seja, .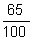

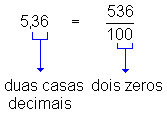
5,36 (lê-se "quinhentos e trinta e seis centésimos"), ou seja,  .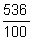

0,047 (lê-se "quarenta e sete milésimos"), ou seja, .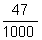

Verifique então que:

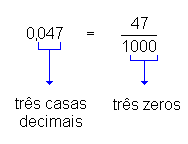
Assim:

Um número decimal é igual à fração que se obtém escrevendo para numerador o número sem vírgula e dando para denominador a unidade seguida de tantos zeros quantas forem as casas decimais.

Transformação de fração decimal em número decimal

   Observe as igualdades entre frações decimais e números decimais a seguir:

  

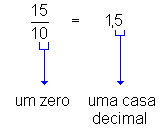
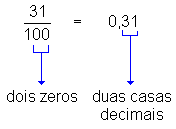
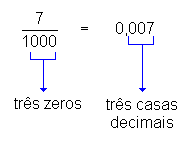
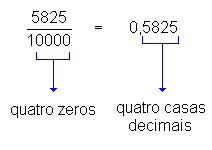
   Podemos concluir então que:

Para se transformar uma fração decimal em número decimal, basta dar ao numerador tantas casas decimais quantos forem os zeros do denominador.

Se ainda não ficou claro, vamos ver o passo a passo, para a transformação:

1.      Conte quantas casas para a direita a vírgula deverá andar para que o número deixe de ser decimal. Por exemplo, no número 12,505 a vírgula deverá andar 3 casas para a direita para deixar de ser decimal e virar inteiro.

2.      O denominador da fração será uma potência de 10, ou seja 10, 100, 1000 etc. O número de casas que contamos no primeiro passo será o número de zeros que acompanhará o 1 no denominador que colocaremos. No exemplo dado, como falávamos de 3 casas, o denominador da fração será o 1 com 3 zeros, ou seja, 1000.

3.      Escrevemos agora a fração onde o numerador é o número original sem a vírgula e o denominador é a potência de 10 obtida no item 2. Para o exemplo dado, teríamos como resultado 12505/1000.

4.      Por fim, se for possível, simplificamos a fração. No exemplo, a fração é simplificável por 5 e o resultado final obtido é, então, 2501/200.

Na próxima aula vamos ver as Dízimas Periódicas e Frações Geratriz.