TRIGONOMETRIA

Boa tarde pessoal, hoje vamos falar sobre uma matéria que é vista como o terror do Ensino Médio, a TRIGONOMETRIA . E de fato é uma matéria bem complexa, que exige o máximo de atenção para que ela consiga ser compreendida, pois ela envolve muitos detalhes que se não forem entendidos no começo, ela vai se tornando cada vez mais complicada.

Hoje vamos ver o que é a Trigonometria, suas propriedades, o conceito envolvendo o triângulo retângulo que é muito importante nessa matéria, vamos ver também que a Trigonometria está presente em nosso dia a dia e no final, vou disponibilizar um vídeo bem bacana do Prof.  Dimas, onde ele faz uma canção para não esquecermos o básico da Trigonometria  e o circulo Trigonométrico. E por fim, vamos ver os Ângulos Notáveis, que recebe esse nome porque são utilizados com mais frequências nos cálculos da Trigonometria.

Preparados para mais uma aula? Então vamos lá (...)

Trigonometria

A trigonometria é a parte da matemática que estuda as relações existentes entre os lados e os ângulos dos triângulos.

Funções Trigonométricas

As funções trigonométricas são as funções relacionadas aos triângulos retângulos, que possuem um ângulo de 90°. São elas: seno, cosseno e tangente.

As funções trigonométricas estão baseadas nas razões existentes entre dois lados do triângulo em função de um ângulo.

Ela são formadas por dois catetos (oposto e adjacente) e a hipotenusa:

Lê-se cateto oposto sobre a hipotenusa.

Lê-se cateto adjacente sobre a hipotenusa.

Lê-se cateto oposto sobre cateto adjacente.

Círculo Trigonométrico

O círculo trigonométrico ou círculo unitário é usado no estudo das funções trigonométricas: seno, cosseno e tangente.

Teoria Euclidiana

Alguns conceitos importantes da geometria euclidiana nos estudos da trigonometria são:

Lei dos Senos

A Lei dos Senos estabelece que num determinado triângulo, a razão entre o valor de um lado e o seno de seu ângulo oposto, será sempre constante.

Dessa forma, para um triângulo ABC de lados a, b, c, a Lei dos Senos é representada pela seguinte fórmula:

Lei dos Cossenos

A Lei dos Cossenos estabelece que em qualquer triângulo, o quadrado de um dos lados, corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles.

Dessa maneira, sua fórmula é representada da seguinte maneira:

Lei das Tangentes

A Lei das Tangentes estabelece a relação entre as tangentes de dois ângulos de um triângulo e os comprimentos de seus lados opostos.

Dessa forma, para um triângulo ABC, de lados a, b, c, e ângulos α, β e γ, opostos a estes três lados, têm-se a expressão:

Teorema de Pitágoras

O Teorema de Pitágoras, criado pelo filósofo e matemático grego, Pitágoras de Samos, (570 a.C. - 495 a.C.), é muito utilizado nos estudos trigonométricos.

Ele prova que no triângulo retângulo, composto por um ângulo interno de 90° (ângulo reto), a soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa:

a² = c²+ b²

Sendo,

a: hipotenusa

c e b: catetos

Curiosidade

O termo "trigonometria", do grego, é a união das palavras trigono (triângulo) e metrein (medidas).

APLICAÇÃO DA TRIGONOMETRIA NO NOSSO DIA A DIA.

Esse ramo da matemática possui uma infinidade de aplicações práticas. Desde a antiguidade já se usava da trigonometria para obter distâncias impossíveis de serem calculadas por métodos comuns. Com a Trigonometria é possível:

- Determinar a altura de um certo prédio.

- Medir a distância da Terra à Lua.

- Quando um engenheiro precisa saber a largura de um rio para construir uma ponte, o trabalho dele fica mais fácil se ele usar os recursos trigonométricos.

- Um cartógrafo, desenhista de mapas, que precisa saber a altura de uma montanha, o comprimento de um rio, etc. Sem a trigonometria demoraria anos para desenhar um mapa.

Na astronomia a Trigonometria é bem utilizada, veja alguns exemplos onde sua aplicação é fundamental:

- Eclipses: No cálculo do tamanho da sombra e no cálculo do raio da sombra.

- Distâncias dentro do Sistema Solar: Calcular distância de planetas inferiores e distâncias de planetas superiores.

- Determinação do raio lunar: Um observador com ajuda de aparelhos especiais que lhe forneçam o ângulo em que ele vê a lua e a distância em que a Lua se encontra da Terra, pode descobrir o raio da Lua, apenas utilizando a lei do seno.

- Determinação da distância Terra-Sol: Para calcularmos a distância da Terra ao Sol, devemos durante o período da fase quarto-crescente da lua, quando o ângulo formado pela terra, a Lua e o Sol for de 90°, afixar três varetas no chão. Com um transferidor medir o ângulo (abc), calcular os lados do triângulo menor, e depois aplicar regra da semelhança entre triângulos.

ÂNGULOS NOTÁVEIS

Os ângulos de 30º, 45º e 60º são chamados de notáveis, pois são os que com mais frequência calculamos.

Sendo assim, é importante conhecer os valores do seno, cosseno e tangente desses ângulos.

Tabela dos ângulos notáveis

A tabela abaixo é muito útil e pode ser facilmente construída, seguindo os passos indicados.

Se ficou complicado de entender, não se preocupe! Preste atenção nessa música para a construção da Tabela dos Ângulos Notáveis:

Vamos fazer atividades para ver se entendemos a matéria.

ATIVIDADES

1-     Determine o valor das incógnitas a seguir:

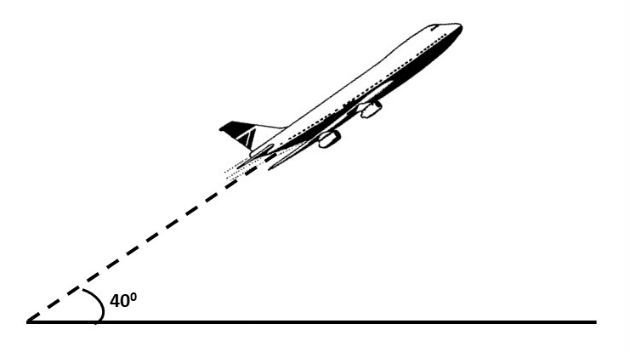
2-     A figura abaixo representa um avião que decolou sob um ângulo constante de 40º e percorreu em linha reta 8000 m. Nesta situação, qual a altura que se encontrava o avião ao percorrer essa distância?

Considere:

sen 40º = 0,64

cos 40º = 0,77

tg 40º = 0,84

3- Uma escada de 2m de comprimento está apoiada no chão e em uma parede vertical. Se a escada faz 30° com a horizontal, a distância do topo da escada ao chão é de:

a) 0,5 m

b) 1 m

c) 1,5 m

d) 1,7 m

e) 2 m

Ótimos estudos!!